Kryptografia – funkcje skrótu, hash i hasła (cz. 1)

Autor:
Zespół Innokrea

Data publikacji: 2023-11-09

Kategorie: Bezpieczeństwo

Dzisiaj chcemy Wam opowiedzieć o kolejnych tajnikach kryptografii – funkcje skrótu, hash oraz hasła, a także ich przechowywanie i generowanie. Spróbujemy zacząć od podstaw i sukcesywnie serwować Wam bardziej skomplikowaną wiedzę w tym temacie. Jeśli jesteście zainteresowani, to zapraszamy do lektury, a jednocześnie zachęcamy do nadrobienia zaległości – jeśli jeszcze nie widzieliście poprzednich artykułów, koniecznie zajrzyjcie do nich.

Czym są i do czego używamy funkcji skrótu?

Funkcje skrótu to takie funkcje matematyczne, które po podaniu ciągu znakowego dowolnej długości zwracają ciąg znakowy o stałej długości np. 256 bitów. Dla każdego ciągu wejściowego jest inny ciąg wyjściowy. Haszowanie jest operacją wskutek której tracimy część informacji, ponieważ możemy przetwarzać długi ciąg na taki o stałej długości. Dodatkowo warto powiedzieć że hashowanie jest nieodwracalne (a przynajmniej nie powinno być) to znaczy znając hash nie powinniśmy być w stanie stwierdzić jaki ciąg został podany.

Przykładami funkcji skrótu są np. MD5, SHA-1, SHA-256, SHA-3 czy BLAKE. Funkcje skrótu są wykorzystywane przy:

podpisach cyfrowych
przechowywaniu haseł w bazie danych
szyfrowaniu z kluczem publicznym
sprawdzenia integralności danych, czyli czy dane nie zostały zmodyfikowane podczas transportu

Każdy użytkownik Internetu nieświadomie korzysta z różnych mechanizmów hashowania podczas łączenia się przez VPN, wchodzenia na strony z kłódką (SSL/TLS) czy programując podczas użycia systemu kontroli wersji (hash’e poszczególnych commitów). Nawet programy antywirusowe sprawdzają tak zwane sygnatury wirusów (dlatego hakerzy stosują wirusy polimorficzne) to tak naprawdę liczą funkcję skrótu podając jako wejście całość lub część kodu wirusa.

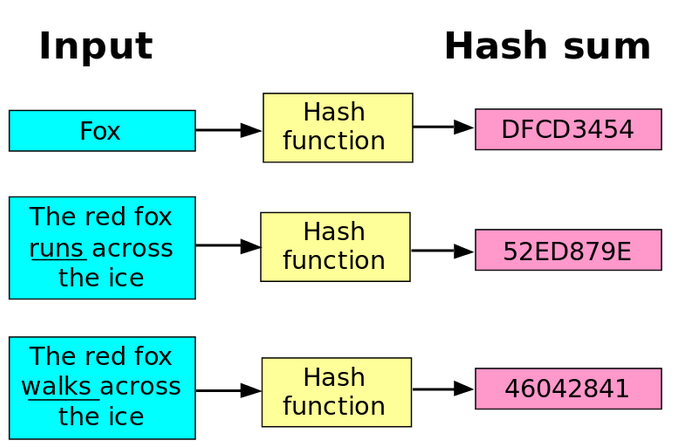
Rysunek 1 – działanie funkcji skrótu, źródło: commons.wikimedia.org

Bezpieczeństwo w funkcjach skrótu

Warto także zaznaczyć, że nie każda funkcja skrótu nadaje się do zastosowania kryptograficznego np. CRC (ang. cyclic redundancy checks) jest stosowana do weryfikacji integralności w sieciach i nie zapewnia żadnego bezpieczeństwa kryptograficznego. Podsumowując, o ile szyfrowanie danych służy do zapewnienia ich poufności o tyle funkcje hashujące mają za zadanie zapewnić integralność danych tj. dowodzą, że dane nie zostały zmienione podczas transport ich przez medium.

Bardzo częstym wykorzystaniem funkcji skrótu jest podpis cyfrowy, w którym po obliczeniu skrótu danej wiadomości szyfruje się kluczem prywatnym jej skrót. Osoba odbierająca komunikat deszyfruje skrót kluczem publicznym wysyłającego, a następnie liczy skrót przesłanej wiadomości. Jeśli wartości się zgadzają to oznacza to, że wiadomość nie została zmodyfikowana i że wysłała ją osoba posiadająca dany klucz prywatny. Podpisanie skrótu komunikatu jest tak samo bezpieczne z punktu widzenia integralności jak podpisanie komunikatu. Większość algorytmów podpisu może pracować jedynie na krótkich danych tj. hashach wiadomości, co jest rozwiązaniem optymalnym.

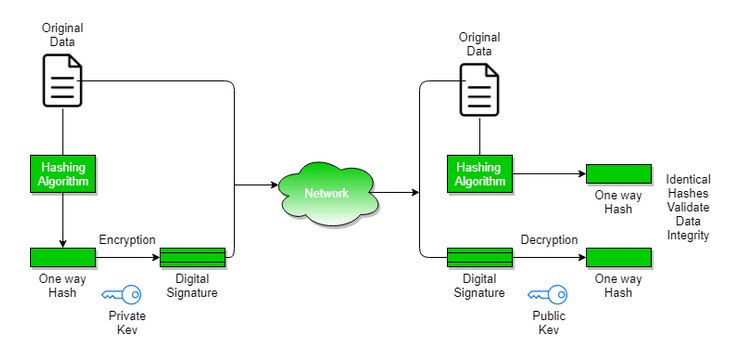
Rysunek 2 – Przesłanie wiadomości podpisanej cyfrowo i weryfikacja podpisu, źródło: geeksforgeeks

Hash: losowość, przeciwobraz i kolizje

Koncepcja funkcji skrótu opiera się na jej losowości i nieprzewidywalności. Dobrze zaprojektowana funkcja skrótu powinna:

- posiadać dużą dyfuzję, co oznacza, że zmiana pojedynczego bitu w wejściu powinna powodować zmianę przynajmniej połowy bitów na wyjściu. Jest to efekt podobny do efektu lawinowego w szyfrowaniu. Bezpieczna funkcja skrótu powinna działać jak czarna skrzynka, która po podaniu pewnego wejścia zdaje się zwracać losowy ciąg na wyjściu, tak aby nie dało się przewidzieć kolejnych wartości przy zmianach kolejnych bitów wejściowych.
- być odporna na przeciwobraz – przeciwobraz (ang. pre-image) danej wartości hash’a H to dowolny komunikat M, którego Hash(M) = H. Oznacza to po prostu, że funkcja powinna być jednokierunkowa tj. niemożliwe jest uzyskanie dowolnego komunikatu z danego wyniku funkcji haszującej. Celem jest zapewnienie, że nie jest łatwo znaleźć oryginalną wartość wejściową, która odpowiada danemu wynikowi funkcji skrótu.
- być odporna na wtórne przeciwobrazy (ang. second pre-image resistance) – oznacza to, że dla wejścia M1 i Hash’a H1 niemożliwe powinno być znalezienie dowolnego drugiego wejścia M2, które ma ten sam wynik co dane wejście tzn. dla M1 != M2 i Hash (M1) = H1 niemożliwe jest znalezienie takiego M2, że Hash(M2) = H1 .
- być odporna na kolizje – wynika to z odporności na wtórne przeciwobrazy, jednak chodzi tu o znalezienie dwóch dowolnych komunikatów wejściowych M1 i M2, dla których istnieje ten sam hash. Funkcja skrótu jest jednak z definicji podatna na kolizje (zasada Dirichleta mówi o tym, że każda taka funkcja musi być kolizyjna ponieważ ma więcej danych wejściowych niż wyjściowych -> https://en.wikipedia.org/wiki/Collision_resistance ). Kolizje powinny być jednak możliwie trudne, a wręcz niemożliwe do znalezienia, w czym pomaga zarówno długość hash’a jak i budowa samej funkcji.

Hash: paradoks dnia urodzin

Z hash’ami i kryptografią związany jest także tak zwany paradoks dnia urodzin. Jest to następująco zadany problem: Jak dużo należy zgromadzić ludzi w jednym pomieszczeniu, aby prawdopodobieństwo urodzenia się dwóch osób w tym samym (dowolnym) dniu wynosiło ponad 50%? Odpowiedź jest zaskakująca. Pomimo, że rok ma 365 dni to wystarczą do tego zaledwie 23 osoby. Co więcej przy 57 osobach jest to już 99% pewności, że dwie z nich urodziły się tego samego dnia. Jak to możliwe? Jeśli jesteście zainteresowani matematycznymi szczegółami stojącymi za tym paradoksem, to polecamy to 3-minutowe wideo. https://www.youtube.com/watch?v=Y_shcEgdhI8

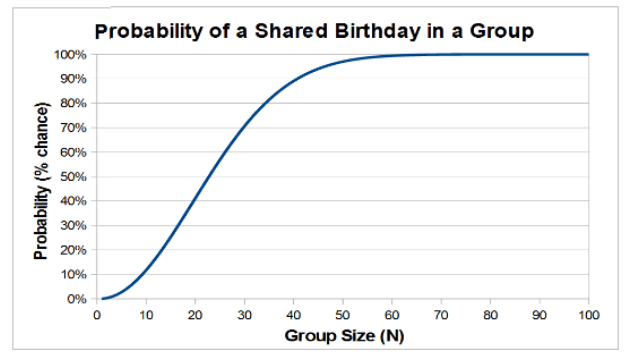
Rysunek 3 – wykres prawdopodobieństwa takiego samego dnia urodzin w zależności od wielkości grupy, źródło: edscave.com

Jeśli chodzi o hash, paradoks dnia urodzin także ma swoje zastosowanie. Jeśli jako liczbę dni w roku przyjmiemy ilość możliwości zapisu różnych liczb na N bitach tj. 2^N, to możemy oszacować ile hash’y musielibyśmy sprawdzić, aby dwa wejścia funkcji skrótu dawały taki sam hash. Używając kalkulatora w Internecie np. https://www.bdayprob.com/ jesteśmy w stanie powiedzieć, że dla 16-bitowego hash’a tj. 2^16 = 65536 możliwych różnych hash’y wystarczy jedynie 300 hash’y by z 50% szansą odnaleźć kolizję.

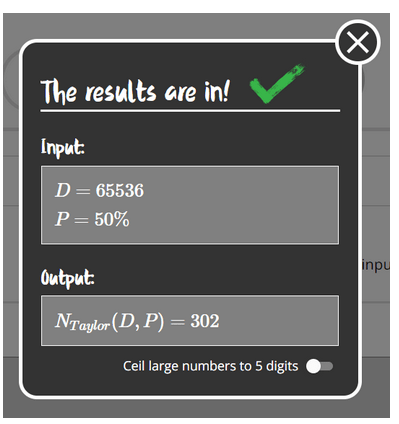
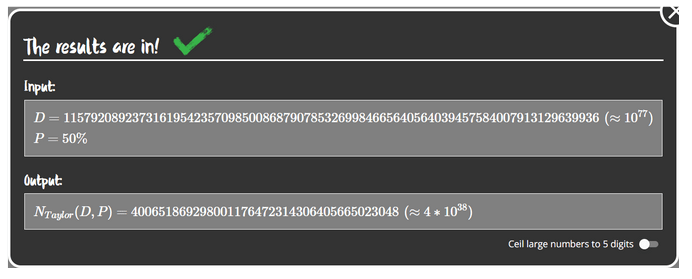
Rysunek 4 – D – liczba dni w miesiącu (u nas liczba możliwych hash’y), P – prawdopodobieństwo kolizji jakie chcemy osiągnąć, Output – minimalna liczba dla osiągnięcia skuteczności 50%

Co jeśli rozpatrzymy tę sytuację dla hash’a 256-bitowego? Ciąg 256-bitowy może być skonstruowany na 2^256 różnych sposobów co w przybliżeniu wynosi 10^77. Aby uzyskać 50% skuteczność należałoby wygenerować 4*10^38 hash’y.

Tak ogromne liczby są nieintuicyjne dla człowieka. Zadajmy sobie więc pytanie jak długo trwałoby znalezienie takiego hash’a, zakładając że mamy do dyspozycji moc sieci komputerów jaką ma bitcoin, czyli ok. 500 exahash’y/s (tj. 500 * 10^18).

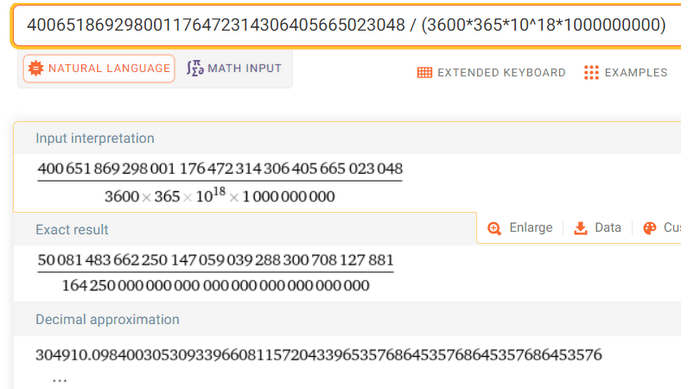
Biorąc pod uwagę te wartości wygenerowanie takiej ilości hash’y zajęłoby 305000 miliardów lat i jest to tysiące razy większa wartość niż wynosi wiek całego wszechświata. Należałoby jeszcze zadać pytanie jaką część wszystkich 256 bitowych hashy trzeba wygenerować, aby osiągnąć hipotetycznie taki efekt. Jest to 1/(4 × 10 ^ -39) * 100% (10^34 razy mniej niż promil). Oznacza to, że nawet jeśli jest to tak niewielki ułamek całości hashy, który należałoby wygenerować, to nasze dzisiejsze możliwości mocy obliczeniowej na to nie pozwalają – a przypomnijmy, że całe rozwiązanie dotyczy odnalezienia kolizji dwóch dowolnych łańcuchów wejściowych i nie uwzględnia sortowania, przeszukiwania i przechowywania takiej ilości danych.

Mówiąc krótko, prawidłowo zaprojektowana funkcja haszująca o długości 256 bitów jest więcej niż bezpieczna jak na dzisiejsze standardy mocy obliczeniowej.

Metoda Rho

Istnieją także bardziej optymalne metody wyszukiwania kolizji, które nie wymagają tak dużej ilości pamięci i obliczeń i jednym z nich jest metoda Rho. Działa ona następująco:

wybierz losowy ciąg znaków i zahashuj go, aby uzyskać wartość początkową.
w pętli hashuj wartość poprzedniego hasha, tworząc łańcuch hashowanych wartości
analizuj skróty w łańcuchu, aż znajdziesz cykl i tym samym kolizję (dwa różne wpisy, które dają ten sam wynik skrótu)

Taka metoda wykorzystuje mniej pamięci niż naiwne zapisywanie i przeszukiwanie losowych wartości. Do znalezienia kolizji potrzeba zwykle 2 ^ (n/2) + 2 ^ (n/2) wykonanych obliczeń, gdzie n to liczba bitów.

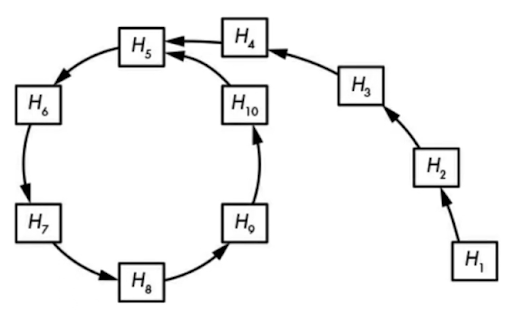
Rysunek – wizualizacja metody Rho, gdzie kolejne strzałki reprezentują obliczanie kolejnych wartości skrótu. Pętla oznacza znaleziony cykl, a wejście H10 oraz H4 daje to samo na wyjściu – H5. źródło – Jean Phelippe Aumasson – Nowoczesna kryptografia

Podsumowanie

Mamy nadzieję, że dzisiejsze rozważania matematyczne Was nie przytłoczyły. Za tydzień kontynuujemy nieco tematy hashowania i zagłębimy się w tematy związane z ich praktycznym zastosowaniem. Do usłyszenia!

Źródła: