Kryptografia – losowość w cyberbezpieczeństwie

Dzisiaj chcemy Wam opowiedzieć o losowości w kryptografii. Czym jest losowość, jak właściwie ją oszacować oraz jak istotna jest w dziedzinie jaką jest kryptografia i której poświęciliśmy ostatnie artykuły. Jeśli jesteście zainteresowani, to zapraszamy!

Losowość – czy jest aż tak istotna?

Dlaczego właściwie kryptografia zajmuje się pojęciem losowości? Odpowiedź na to pytanie jest bardzo prosta. Zajmuje się, ponieważ losowość leży u podstaw większości konceptów w całej dziedzinie kryptografii: w generowaniu kluczy, tzw. soli, wektorów inicjalizujących, a także w systemach szyfrujących czy nawet podczas ataków na systemy kryptograficzne.  Jeśli działania kryptograficzne są przewidywalne, a tym samym nielosowe oznacza to, że dane działanie jest z definicji niebezpieczne. 

Intuicja zawodzi

Intuicyjnie, nasze umysły wydają się być w stanie określić, czy pewien ciąg znaków jest losowy. W przypadku długich ciągów znakowych np. 128 bitowych kluczy jest to jednak niemożliwe. Ponadto podczas intuicyjnego rozumowania o losowości popełniamy zwykle dwa rodzaje błędów:

• zakładamy, że coś jest losowe, ponieważ wygląda na losowe i nasz mózg nie dostrzega w tym żadnego wzorca
• zakładamy, że za losowo pojawiającymi się wzorcami stoi jakiś wzór lub schemat.

W praktyce, w celu pozyskania ciągów, które są losowe używamy działu matematyki związanego z prawdopodobieństwem i statystyką  (rozkładami liczb). Procesy zachodzące w przyrodzie czy doświadczenia mają pewne rozkłady prawdopodobieństwa np. jeśli rzucamy prawidłowo wyważoną monetą z prawdopodobieństwem ½ uzyskujemy reszkę i z prawdopodbiestem ½ uzyskujemy orła. Rozkład prawdopodobieństwa sumuje się do 1, ponieważ zgodnie z definicją prawdopodobieństwa wartość 1 oznacza pewność wystąpienia zdarzenia (1 oznacza 100% prawdopodobieństwa). Rozkład prawdopodobieństwa rzutu wyważoną monetą jest jednorodny, ponieważ każde zdarzenie (orzeł i reszka) są tak samo prawdopodobne (½).  Generując kolejne zera i jedynki w kryptografii można o nich myśleć jak o kolejnych rzutach monetą.

Odróżnienie ciągów wyglądających na losowe od tych naprawdę losowych jest podstawą bezpieczeństwa w kryptografii. Stosowanie pseudolosowości zamiast losowości niszczy cały system kryptograficzny u samej podstawy.

Entropia – miara niepewności

Zgodnie z definicją do formalnego określenia będziemy potrzebować pojęcia rozkładu prawdopodobieństwa, które przypisuje poszczególnym zdarzeniom w procesie losowym wartości prawdopodobieństwa np. rozkład rzutu monetą to ½ prawdopodobieństwa dla orła i ½ dla reszki. Prawdopodobieństwa w rozkładzie muszą sumować się do wartości 1 (zgodnie z definicją prawdopodobieństwa).

Entropia natomiast jest miarą niepewności lub nieuporządkowania systemu. Im większa entropia tym większa niepewność co do wyników. 

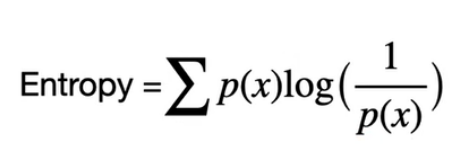
Rysunek 1 – Suma po prawdopodobieństwach poszczególnych zdarzeń razy “miara zaskoczenia”. Logarytm ma w podstawie liczbę 2 (logarytm binarny) – jest to tzw. entropia Shannona.

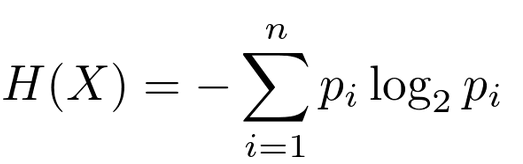
Rysunek 2 – Częściej spotykana w literaturze forma wzoru z rysunku 1, źródło: towardsdatascience.com

Drugi składnik we wzorze log(1/p(x)) może być postrzegany jako miara naszego zaskoczenia. Jeśli np. wykonujemy rzuty nierówną monetą w którym prawdopodobieństwo wyrzucenia orła wynosi ⅛ a reszki ⅞ to:

Entropy = ⅛ * log(1/(⅛)) + ⅞*(log(1/(⅞)) = ⅛ * 3 + ⅞ * 0.193 = 0.375 + 0.169 = 0.544

Jeśli wypadnie nam orzeł to nasze “zaskoczenie” wynosi 3 a jeśli reszka to zaledwie 0.193. Wynika to z tego, że mniej spodziewamy się wypadnięcia orła, bo prawdopodobieństwo takiego zdarzenia jest stosunkowo niewielkie (zaskoczenie jest odwrotnie proporcjonalne do prawdopodobieństwa danego zdarzenia).

Rozważmy jeszcze przykład entropii w klasycznej monecie:

Entropy = ½ * log(1/(½)) + ½ * log(1/(½)) = ½ *1 + ½ * 1 = 1

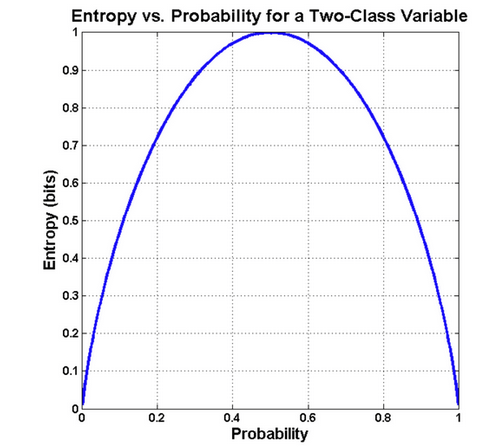
Rysunek 3 – funkcja entropii dla rzutu monetą w zależności od wybranego rozkładu prawdopodobieństwa. – źródło: bytepawn

Na rysunku możemy zaobserwować, że największa entropia (miara niepewności) jest dla rozkładu jednorodnego, czyli takiego gdzie prawdopodobieństwa zdarzeń są równe (½ dla każdej ze stron monety). Entropia jest maksymalna, gdy rozkład jest jednorodny, bo żaden wynik nie jest wtedy bardziej prawdopodobny od innych.

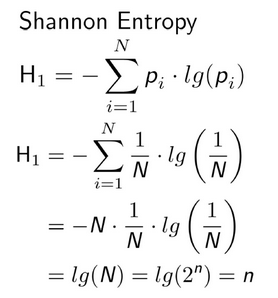
Rysunek 4 – Wzór na entropię można przy rozkładzie jednorodnym uprościć w następujący sposób (pi= 1/N , N = 2^n (n bits)), źródło osti.gov

Oznacza to więc, że dla klucza np. 128 – bitowego w kryptografii, którego generator posiada rozkład jednorodny entropia wynosi n – bitów. 

Pomyślmy przez chwilę o haśle składającym się z 8 bajtów (64 bity). Maksymalnie takie hasło może mieć 64 bity entropii. Intuicyjnie, aby mieć dostateczne szanse na złamanie tego hasła, trzeba by losowo wypróbować połowę tych możliwości, co jest równoznaczne z 2^64 / 2 = 2^63 kombinacjami. Oznacza to 9.223372e+18 prób. Jeśli natomiast założymy, że to hasło może być słowem z słownika, to możliwości zmniejszają do zaledwie kilkuset tysięcy możliwości. Mamy więc wtedy rozkład nierównomierny, bo słowa używane w języku są bardziej prawdopodobne niż te wyglądające na losowe – oznacza to mniejszą entropię, czego efektem może być znacznie łatwiejsza możliwość złamania takiego hasła. Dlatego właśnie, w celu zapewnienia naszym danym jak największej ochrony, powinniśmy korzystać z generatorów haseł (będących często częścią menadżerów haseł), zamiast używać łatwych do zapamiętania, ale i niebezpiecznych słów ze słownika.

Wyobraźmy sobie sytuację, że chcemy wysłać nasze tajne hasło do kolegi i w tym celu szyfrujemy je współdzielonym kluczem (psk, ang. pre-shared key). Ktoś przechwytuje naszą wiadomość i próbuje zgadnąć klucz. Jeżeli utworzone przez nas hasło ma niską entropię (czyli na przykład jest słowem ze słownika), to atakującemu, który próbuje odszyfrować ciphertext pewnym kluczem będzie łatwo stwierdzić, że znalazł właściwy klucz i posiada poprawne hasło. Jeśli natomiast pierwotna wiadomość miała wysoką entropię, to po zdeszyfrowaniu kolejnymi zgadywanymi kluczami wiadomość nadal nie będzie dla człowieka czytelna (nie będzie żadnym “zrozumiałym” słowem) – stąd nie będziemy mieli pewności czy jest to tekst którego faktycznie szukamy. Ten przykład ma sens tylko jeśli atakujący zna długość klucza i długośc klucza jest mniejsza niż długość przesyłanej wiadomości.

OTP – One-time pad

Powyższy przykład dotyczący entropii ilustruje także dlaczego szyfr z kluczem jednorazowym jest bezpieczny. Taki szyfr polega właściwie na tym samym co szyfr Cezara, tylko z każdą literą/bitem mamy inną wartość dla klucza. Oznacza to, że dla każdej wiadomości długości n-bitów należałoby posiadać inny n-bitowy klucz (a więc dla zaszyfrowania dysku 500 GB należałoby posiadać klucz o długości 500 GB). Taki szyfr nie jest praktyczny, ale należałoby zrozumieć dlaczego mówi się o nim, że jest szyfrem o idealnej tajności. Jeśli napastnik dysponuje nieograniczoną mocą obliczeniową nie jest w stanie odgadnąć pierwotnego tekstu, co w latach 40 ubiegłego wieku wykazał Claude Shannon. 

Można tu przytoczyć dość obrazowy przykład pana Francis Litterio (link do jego pełnego artykułu w opisie).

“Jeśli klucz jest naprawdę losowy, one-time pad oparty na operacji XOR jest całkowicie odporny na ciphertext-only attack (kryptoanaliza na podstawie szyfrogramu). Oznacza to, że atakujący nie może poznać tekstu jawnego na podstawie szyfrogramu bez znajomości klucza, nawet poprzez atak bruteforce, czyli przeszukiwanie przestrzeni wszystkich kluczy. Wszystkie możliwe teksty jawne są równie prawdopodobne. 

Załóżmy, że przechwyciłeś bardzo mały, 8-bitowy szyfrogram. Wiesz, że to albo 8 bitowy znak ASCII 'S’, albo znak ASCII 'A’, zaszyfrowany z użyciem one-time pad. Wiesz również, że jeśli to 'S’, wróg zaatakuje od strony morza, a jeśli to 'A’, wróg zaatakuje z powietrza. To wiele informacji. Brakuje ci tylko klucza, głupiego małego 8-bitowego jednokrotnego klucza. Zlecasz swojemu zespołowi kryptologów wypróbowanie wszystkich 256 możliwych 8-bitowych kluczy jednokrotnych (2^8 kombinacji) czyli atak bruteforce. Wynikami przeszukiwania przestrzeni kluczy jest to, że twój zespół znajduje jeden 8-bitowy klucz, który deszyfruje szyfrogram na 'S’, i jeden, który go deszyfruje na 'A’. I nadal nie wiesz, który z nich to rzeczywisty tekst jawny. To argument, który można łatwo uogólnić na klucze (i teksty jawne) o dowolnej długości.”

Pomimo że OTP teoretycznie doskonały, jego praktyczna implementacja napotyka wiele wyzwań. Generowanie naprawdę losowych kluczy o tej samej długości co wiadomość jest trudne. Dodatkowo, bezpieczne udostępnianie i zarządzanie tak długimi kluczami może być logistycznie skomplikowane. Na wikipedii można jednak poczytać o historycznych użyciach OTP, między innymi przez szpiegów KGB (link w źródłach).

Generatory liczb losowych TRNG vs PRNG

U podstaw bezpieczeństwa systemów kryptograficznych leży, jak już ustaliliśmy, losowość. Dowiedzieliśmy się, że największa entropia jest przy rozkładzie jednorodnym. Jak jednak generować liczbę, która jest naprawdę losowa? Potrzebny jest pewien komponent, który jest źródłem losowości. Potrzebujemy do tego dwóch rodzajów RNG (Random number Generator):

• TRNG (ang. True Random Number Generator) – źródło entropii 
• PRNG (ang. Pseudo Number Generator) – algorytm kryptograficzny który generuje jakościowe losowo bity ze źródła entropii
  
  

Źródłem entropii może być komponent, który czerpie ze środowiska analogowego tj. nieprzewidywalnego np. z wykorzystaniem temperatury, szumu akustycznego, elektryczności lub ruchu myszą. TRNG tworzą bity w sposób niedeterministyczny bez gwarancji wysokiej entropii, wolno i nie na żądanie. Dodatkowo, w przyrodzie duża część zjawisk posiada dystrybucję Gaussa, która nie jest rozkładem jednorodnym – musi więc istnieć mechanizm przekształcający rozkład prawdopodobieństwa na bardziej równomierny. Takie działanie nazywamy post-processingiem i jest ono przedmiotem wielu badań.

PRNG natomiast korzystają z TRNG i po pozyskaniu kilku losowych bitów TRNG z użyciem algorytmów i zaawansowanej matematyki przekształcają źródło na długi strumień wiarygodnych, losowych bitów. Generator PRNG otrzymuje, więc w regularnych odstępach czasowych do bufora bity pozyskane przez TRNG i generuje nowy ciąg już w sposób deterministyczny. Połączenie tych dwóch podejść sprawia, że jesteśmy w stanie zapewnić odpowiednią losowość i sprawiać, że nasze klucze są unikalne, a co za tym idzie – systemy kryptograficzne także.

Czy na pewno jesteśmy bezpieczni?

W 2012 roku badacze podjęli się analizy certyfikatów i kluczy publicznych w Internecie z usług SSH i HTTPS. Okazało się, że wiele systemów ma identyczne lub podobne klucze, ponieważ stosowane tam algorytmy opierały się na tych samych czynnikach losowych. Czynniki te były generowane przy starcie systemu, kiedy RNG nie pozyskał jeszcze wystarczających danych zapewniających odpowiednią entropię. Różnice w kluczach wynikały z dodatkowej entropii dodawanej programowo z użyciem PRNG, ale był to proces odwracalny. Polecamy zapoznanie się z poniższym artykułem, a szczególnie stroną 13 na której opisane są porady dla deweloperów. Do usłyszenia za tydzień!

https://www.usenix.org/system/files/conference/usenixsecurity12/sec12-final228.pdf 

Źródła:

• https://pl.wikipedia.org/wiki/Szyfr_Cezara 
• https://www.youtube.com/watch?v=YtebGVx-Fxw 
• https://bytepawn.com/what-is-the-entropy-of-a-fair-coin-toss.html
• https://www.quora.com/What-is-entropy-in-terms-of-cryptography 
• https://towardsdatascience.com/entropy-is-a-measure-of-uncertainty-e2c000301c2c 
• https://securityaware.wordpress.com/2008/07/15/art/ 
• https://en.wikipedia.org/wiki/One-time_pad
• https://crypto.stackexchange.com/questions/31084/how-is-the-one-time-pad-otp-perfectly-secure 
• https://youtu.be/2_w9l9visH8
• https://en.wikipedia.org/wiki/Hardware_random_number_generator 
• https://iacr.org/archive/fse2007/45930135/45930135.pdf 
• https://youtu.be/-h_rj2-HP2E